Tämän kirjoituksen aihe vaatii ehkä enemmän taustatietoja ja on sisällöltään teknisempi. Alkuperäinen ajatus ei myöskään ole minun, vaan on pyörinyt internetissä jo kymmeniä vuosia.
Alkuluvut ja säännölliset lausekkeet
Otsikko näyttää lähinnä siltä, että kissa olisi pomppinut näppäimistöllä. Ymmärtääkseen pitäisi tietää mitä ovat säännölliset lausekkeet ja alkuluvut. Aloitetaan helpommasta.

Alkuluku on sellainen luku, jota ei voi jakaa millään muulla luvulla, kuin ykkösellä ja itsellään. Esimerkiksi luku 5. Jos sen koittaa jakaa luvulla 2, 3 tai 4, jako ei mene tasan. Tällöin ainoat jakajat ovat 1 ja 5 ja tämä tekee luvusta 5 alkuluvun. Myös luku 23022023 on alkuluku: sitä ei voi jakaa millään muulla, kuin ykkösellä ja itsellään. Alkuluvut ovat loputtoman mielenkiintoisia jo itsessään, mutta ei käsitellä niitä nyt sen tarkemmin. Alkuluja täytyy etsiä, sillä moderni tiedon salaaminen perustuu niihin: ilman alkulukuja ei pääse verkkopankkiin, eikä sähköpostiin. Tämäkin olisi hyvin kiinnostava aihe, mutta tämän kirjoituksen varsinainen aihe on alkulukujen etsintä vähän epätavallisemmalla menetelmällä.
Miten ihmeessä sitten otsikon mysteerisotku ^(11+)\1+$ löytää alkulukuja?
Unaariset numerot
Tavallisia lukuja kirjoitamme kymmenellä merkillä, eli kaikille tutuilla numeroilla 0-9. Kun numerot loppuvat kesken, uusia lukuja merkataan yhdistelemällä näitä kymmentä symbolia. Numeron 9 jälkeen ei siis tule mikään uusi merkki, vaan yhdistellään vanhoja, joten seuraava luku on 10. Aika selkeää.
Binääriluvuissa käytössä on vain kaksi merkkiä, 0 ja 1. Tämä on tietokoneelle sopiva muoto, koska nämä kaksi lukua on helppo toteuttaa sähköisesti: virta pois = 0, virta päällä = 1. Jos mennään vielä pidemmälle, niin unaarisessa järjestelmässä käytössä olisi vain yksi merkki, eli 1. Tällöin luvut esitettäisiin siis vain ykkösten jonoina, niin monta ykköstä kuin luvun arvo on. Järjestyksessä ensimmäiset luvut olisivat siis 1, 11, 111, 1111. Vähän kuin roomalaiset numerot, mutta tässä muita merkkejä ei siis tulisikaan. Tässä vielä lisää lukuja unaarijärjestelmällä, yksi kullakin rivillä:
1 11 111 1111 11111 111111 1111111 11111111 111111111 1111111111 11111111111 111111111111 1111111111111 11111111111111
Ennen kuin ihmetellään säännöllisiä lausekkeita, tutkitaan esimerkiksi lukua 12. Unaarijärjestelmässä se kirjoitettaisiin muodossa 111111111111. Kuin lapsi lukuja opetellessaan, voisimme mekin ottaa esiin vaikka tulitikkuja, palikoita tai tässä sähköisesti ihan vain peräkkäisiä ykkösiä ja järjestellä niitä eri kokoisiin ryhmiin. Luvun 12 voisi jakaa monellakin eri tavalla: 3x4 tai 4x3 tai 2x6 tai 6x2:
3 x 4
1111 1111 1111
4 x 3
111 111 111 111
2 x 6
111111 111111
6 x 2
11 11 11 11 11 11
Luku 17 on puolestaan alkuluku. Sitä ei voi jakaa muulla kuin itsellään ja ykkösellä. Ei siis ole mahdollista muodostaa keskenään yhtä suuria ryhmiä, paitsi tietenkin nämä:
1x17
11111111111111111
17x1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
Säännöllinen lauseke
Säännöllinen lauseke on työkalu tekstin täsmäykseen: onko teksti tietyssä muodossa? Kyseessä on esimerkiksi lähes kaikkiin ohjelmointikieliin toteutettu ominaisuus. Aihe on varsin laaja, mutta katsotaan pari esimerkkiä.
p.kka- Pisteen kohdalle voi laittaa minkä tahansa merkin. Tämä siis tunnistaisi sanat “pakka” ja “pokka”. Toki myös “pzkka”. Piste on siis yksittäinen mikä tahansa merkki.
p[ao]kka- Sulkeiden sisältä valitaan täsmälleen yksi merkki. Tämä siis tunnistaa pelkästään sanat “pakka” ja “pokka”.
piz+a- Plus-merkki tarkoittaa, että edellinen merkki miten monta kertaa tahansa, mutta vähintään kerran. Tämä siis tunnistaa esimerkiksi piza, pizza, pizzzzza.
Paljon muitakin ominaisuuksia löytyy. Aidosti hyödyllinen esimerkki voisi olla seuraava: .+@.+\..+. Tämä tai vastaava löytynee kaikilta sivuilta, joihin pitää syöttää kelvollinen sähköpostiosoite. Katsotaan pala kerrallaan:
.+Eli mitä tahansa, vähintään kerran.@Ei erityismerkitystä, kirjaimellinen @-merkki..+Sama kuin yllä.\.Pisteellä on erityismerkitys, mutta edeltävä \- merkki poistaa sen. Tämä siis tarkoittaa kirjaimellista pistettä..+Jälleen sama kuin edellä.
Esimerkiksi siis erkki@esimerkki.fi voidaan tunnistaa tämän lausekkeen avulla: jotain, @-merkki, jotain, piste, jotain. Toisaalta tämä tunnistaa myös tekstin a£%aa@asd.7 joka ei kyllä ole kelvollinen osoite. Tämän takia sivustot lähettävät sähköpostia: ne haluavat varmistaa, että sähköpostiosoite on oikea ja että sinulla on pääsy siihen. Säännöllisellä lausekkeella voisi toki myös vaatia käyttämään pelkkiä kirjaimia, esimerkiksi [a-z]@[a-z]\.[a-z], vaan entäpä sitten numerot tai muut osoitteessa kelvolliset merkit? Ei jumiuduta liiaksi tähän, vaan siirrytään aiheeseen.
^(11+)\1+$
Miten tämä sitten tunnistaa alkuluvun? No ei se tunnistakaan, mutta se tunnistaa ei-alkuluvut, eli komposiittiluvut (yhdistetyt luvut). Koska käsittelemme alkulukuja unaarijärjestelmässä, voimme ajatella niitä vaan tekstinpätkinä, joiden tunnistamiseen säännöllinen lauseke sopii. Varsinaisia laskuoperaatioita ei tarvita.
Sekaannusten välttämiseksi muutetaan alkuperäistä lauseketta hiukan: ^(AA+)\1+$. Esitetään luvut vastaavasti myös A-kirjaimina:
A AA AAA AAAA AAAAA AAAAAA .........
Aiemmassa kappaleessa todettiin, että luvut, jotka eivät ole alkulukuja, voidaan jakaa yhtä suurin ryhmiin. Tässä piilee säännöllisen lausekkeen ajatus alkulukujen tunnistamiseen. Käsitellään lauseke vaiheittain.
A
Aloitetaan kirjaimellisesta A-merkistä.
AA+
Lisätään toinen A ja sille + -merkki, eli tämä jälkimmäinen A voi olla vähintään kerran, mutta enintään loputtomasti.
Tässä kohtaa lausekkeemme tunnistaa esimerkiksi AA, AAA, AAAA mutta ei A.
Määritellään tämä pätkä ryhmäksi, lisäämällä sulkeet:
(AA+)
Ryhmän tarkoitus on esimerkiksi poimia täsmätystä tekstistä vain tietty pätkä, mutta siihen voi myös viitata lausekkeen myöhemmässä vaiheessa. Koska kyseessä on vasemmalta laskettuna ensimmäinen määritelty ryhmä, siihen voidaan viitata merkitsemällä \1:
(AA+)\1.
Nyt tekstissä pitää siis olla vähintään kaksi A:ta ja sen jälkeen täsmälleen sama ryhmä uudelleen. Esimerkiksi jonossa AAAAAA tämä toteutuu:
AAAAAA
Mutta jonossa AAAAA ei:
AAAAA
Vaan entä AAAAAAAAA? Lisätään vielä yksi asia:
(AA+)\1+
Nyt löydetty ryhmä saa esiintyä tarvittaessa monta kertaa, mutta vähintään kerran.
AAAAAAAAA
Nyt lauseke tunnistaa siis A-jonot, jotka voidaan jakaa kahteen tai useampaan yhtä pitkään osaan, siten, että jokaisen osion pituus on vähintään 2 merkkiä pitkä. Sen kummempaa ei tarvita: alkuluja ei voida jakaa, muut luvut voidaan. Jos säännöllinen lauseke täsmää tiettyyn jonoon, sen jonon kuvaama luku ei ole alkuluku.
Jos unaarilukuja haluaa merkata ykkösellä, voi A:n tilanne vaihtaa 1, kuten otsikossa ja aiemmissa esimerkeissä. Jätin sen pois siksi, että myöhemmin tuleva \1 voi aiheuttaa sekaannusta, kun nyt kyse ei olekaan ykkösestä, vaan ryhmäviittauksesta numero 1.
Pari juttua vielä
Parempi muoto lausekkeelle olisi otsikossakin oleva ^(11+)\1+$ tai vielä mieluummin ^1$|^(11+)\1+$
^ viittaa rivin alkuun ja $ viittaa rivin loppuun. Tämä voi olla oleellista jossakin tilanteissa. Säännöllistä lauseketta suorittava ohjelma voi etsiä vastaavuuksia koko syötteestä, ja löytää esimerkiksi luvusta 1111111 vastaavuuden: 1111111. Merkeillä ^$ varmistetaan siis, että etsitään nimenomaan rivin alusta ja loppuun, jolloin koko “sanan” täytyy täsmätä.
Jälkimmäisessä sitten taas huomioidaan poikkeustapaus. Lauseke löytää ne luvut, jotka eivät ole alkulukuja, eikä luku 1 ole alkuluku. Tässä | merkki tarkoittaa “tai”. Etsitään siis ykköstä — joka on yksinään koko rivillä, eli ^1$ — tai sitten toistuvia sarjoja.
Säännöllisiä lausekkeita voi testata esimerkiksi osoitteessa regex101.com, josta löytyy kätevä testausnäkymä selityksineen.
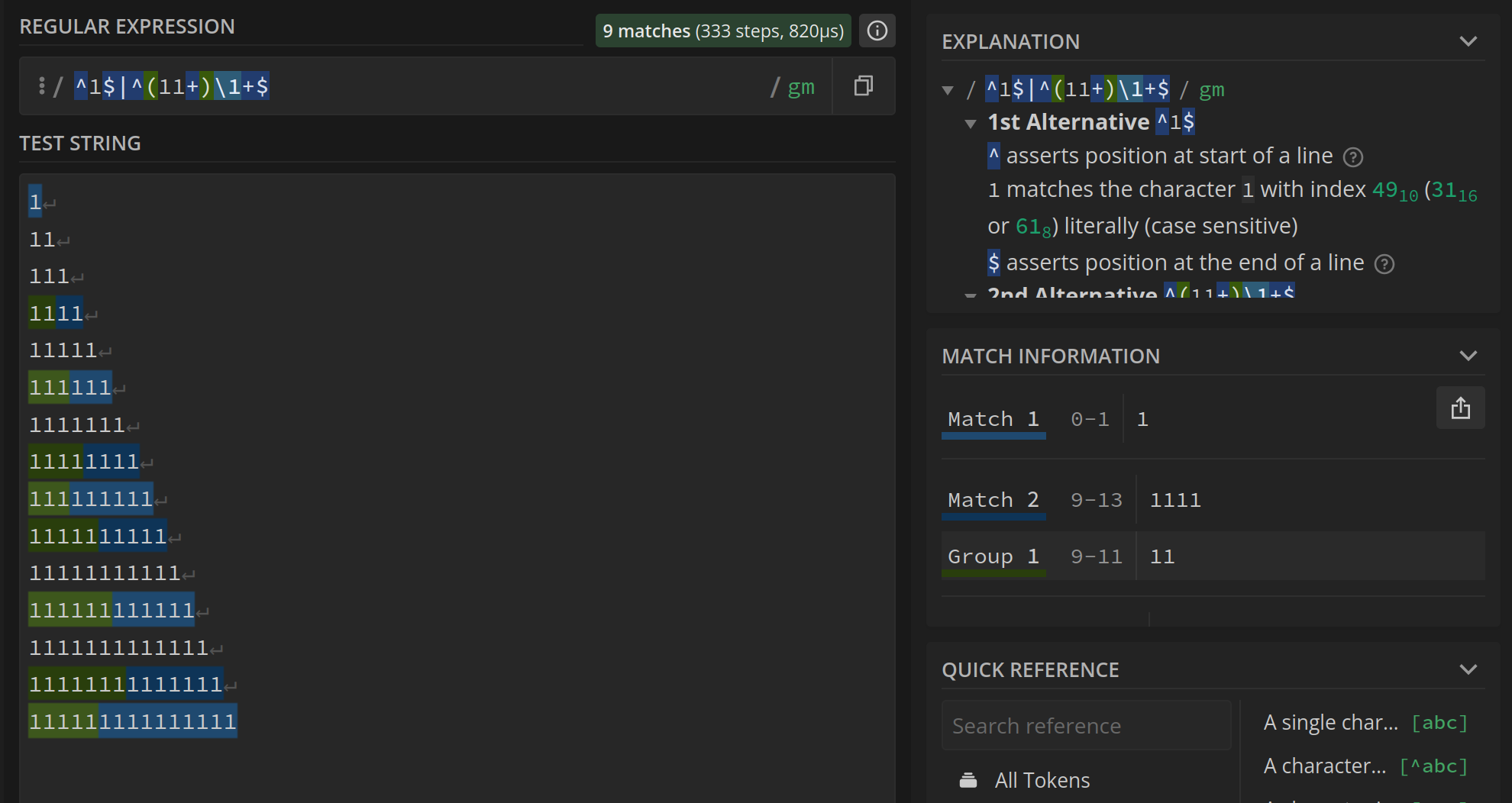
Kaikessa huvittavuudessaan tämä on todella epätehokas tapa etsiä alkulukuja, mutta kiinnostava esimerkki siitä, miten on mahdollista “laskea” järjestelmällä, jota ei varsinaisesti ole suunniteltu laskemiseen.
