Törmäsin kuvassa näkyvään pulmapeliin työpaikalta löytyneen Tek-lehden numerossa 4/2025.

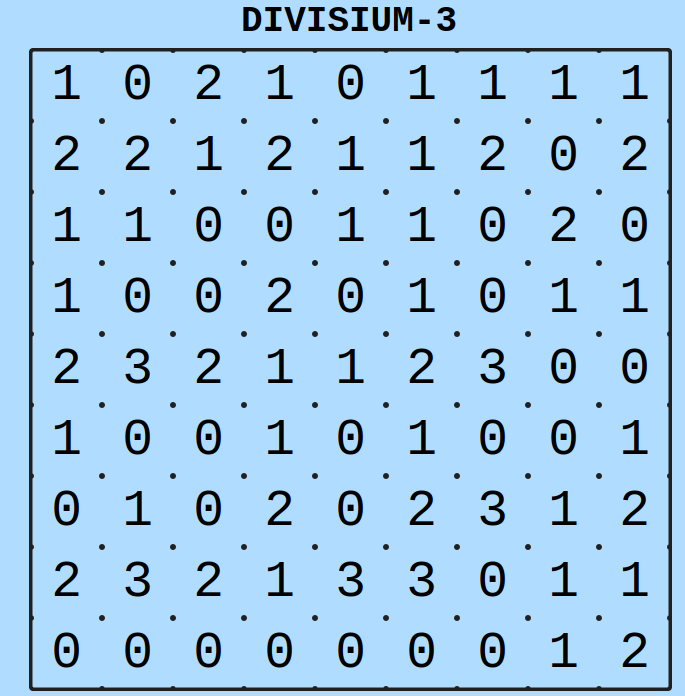
Googlailulla löytyi myös Vesa Timosen tekemä Web-versio, jonka pelaamiseen kuluikin yksi varsin riehakas perjantai-ilta.

Pelin idea lyhyesti: jaa ruudukko täsmälleen 3 ruudun kokoisiin alueisiin, joiden sisältämien lukujen summa on 3. Ratkaisu on yksikäsitteinen, eli pulman voi ratkaista vain yhdesllä tavalla.

Tähän mennessä pelaaminen on osoittanut, ettei pelissä tarvitse koskaan kokeilla: aina pystyy päättelemään yhden alueen. En toisaalta olen ihan täysin varma, kuinka pitkiä päättelyketjuja tarvitsee tehdä, mutta toistaiseksi ne ovat olleet hyvin lyhyitä.

Kannattaa kokeilla peliä ensin itse, jos se kiinnostaa. Osa pelin hauskuudesta oli mielestäni siinä, että pelatessa pystyi löytämään erilaisia sääntöjä ja loogisia päättelyketjuja.

Pelattuasi voit lukea tätä pidemmälle. Keräsin tähän alle joitakin huomaamiani “sääntöjä”, joita seuraamalla pystyy eliminoimaan tiettyjä vaihtoehtoja. Tämän artikkelin lopusta löytyy myös linkki koodiin, jonka avulla pelin voi ratkaista ohjelmallisesti.

Divisiumin ratkaisu

Koska alueen summan pitää olla 3, on jokaiselle alueelle olemassa täsmälleen 3 eri vaihtoehtoa:

• [0,0,3]
• [1,1,1]
• [0,1,2]

Näistä vaatimuksista pystyy löytämään tiettyjä sääntöjä, joita seuraamalla pelialueelle pystyy vetämään viivoja, vaikkei kokonaisia alueita vielä saisikaan ratkaistua. Tästä on apua, sillä tämän avulla tietyt vaihtoehdot voi saada eliminoitua pois.

Sääntö 0

Kaksi nollaa ei voi olla samassa ryhmässä, jos niiden naapurissa ei ole lukua 3.

Koska ainoa ryhmä, jossa on kaksi nollaa, on 0,0,3, kuvassa näkyviä nollia ei voi laittaa samaan. Jos nollat olisivat samassa, ainoa vaihtoehto olisi lisätä ryhmään joko 1 tai 2, jolloin koko olisi jo 3, mutta summa ei.

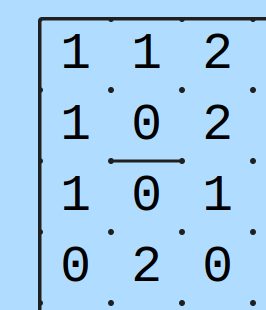
Sääntö 0.1

Edellisen tarkennukseksi, seuraavassa kuvassa on myös sama tilanne. Vaikka kolmonen onkin lähistöllä, kuvassa erotettujen nollien vasemmalla puolella oleva nolla ei voi kuulua minkään kolmosen kanssa samaan ryhmään. Täten se ei voi kuulua toisen nollakaan kanssa (Sääntö 1), eli näiden välissä on varmasti viiva.

Sääntö 1:

Lukupari, jossa molemmat > 1, eivät voi olla samassa ryhmässä. Luvut 3 ja 3 olisivat 6, ssekä luvut 2 ja 2 olisivat 4, eli ryhmän summa olisi taas >3. Nämä voidaan aina erottaa toisistaan viivalla.

Sääntö 2:

Kolmosen kanssa ei voi olla mitään muita positiivisia numeroita >0, koska tällöin summa olisi vähintään 4. Nämäkin voidaan suoraan erottaa toisistaan.

Sääntö 3:

Ykköspari ei voi olla samassa ryhmässä. Ainoa ryhmä, jossa olisi kaksi ykköstä, vaatii kolmannen ykkösen. Tällöin näiden kahden ykkösen on pakko olla eri ryhmissä.

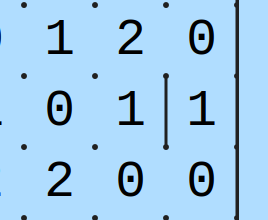
Sääntö 4:

0 ja 1 eivät voi olla samassa ryhmässä, jos kummankaan vieressä ei ole lukua 2. Ainoa ryhmä, jossa vois olla 0 ja 1 samaan aikaan, on [0, 1, 2]. (Kiitokset vaimolleni tämän säännön muotoilusta).

Kuvassa aivan jokaista ei ole merkattu ja kuvat ovat muutenkin vain osittaisia pelialueita. Kuitenkin on hyvä huomata, miten vasemman yläreunan kakkoset voivat potentiaalisesti useampien eri ykkösten kanssa samassa ryhmässä, joten jokaista 0-1 yhdistelmää ei voi rajata.

Sääntö 5:

Ratkaisun yksikäsitteisyysolettama voi joskus auttaa. Pidän tätä vähän epämukavana sääntönä, mutta se on kylläkin toiminut tähän asti.

Oletetaan, että pelialueella esiintyy tilanne, jossa on rajattu vasemmassa reunassa näkyvä 2x3 kokoinen alue. Tämä rajattu alue on siis omalla tavallaan täysin eristyksissä muusta pelialueesta: tämän sisällä voimme tehdä rajauksia ilman, että ne vaikuttavaat ulkopuolelle. Ongelma: vasemman reunan tilanteen voi rajata kahdella eri tavalla:

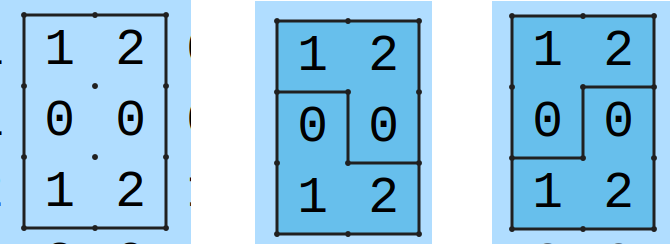
Tämä siis tarkoittaa, ettei pulmalla ole yksikäsitteistä ratkaisua, eli ratkaisuvaihtoehtoja olisi ainakin kaksi erilaista. Ne voisivat olla muuten täysin samat, mutta ainoa ero olisi se, että tietyn 2x3 alueen sisällölle olisi kaksi eri järjestystä.

Johtopäätös: Alkuperäinen 2x3 rajaus ei ole oikein, koska peliä ei voi enää ratkaista täsmälleen yhdellä tavalla.

Johdannasia:

2-0 -parit:

Jokainen 2 tarvitsee aina luvun 0. Jos ei meinaa löytyä yhdisteltävää, tutki, onko jollakin kakkosella vain yksi mahdollinen 0. Tämä ei välttämättä ratkaise vielä mitään, mutta tällöin kyseinen 0 on “varattu” tälle kakkoselle. Tämä voi auttaa huomaamaan, että jokin toinen 2 on pakko kytkeä johonkin toiseen 0:aan.

Toimii myös toiseen suuntaan, eli nollalla on pakko olla jokin 2 (ks. esimerkkipeli alempaa).

Esimerkkitilanne:

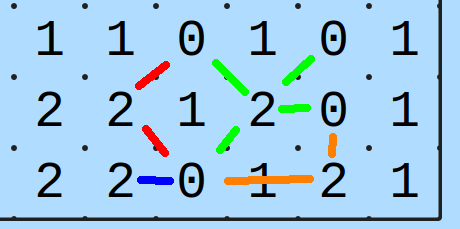
Sinisellä yhdistetty 2-0 on ainoa vaihtoehto kyseiselle 2:lle. Tämän johdosta selviää, että sekä punaiselle, että oranssille on vain yksi 0 enää jäljellä. Tämän jälkeen taas on selvää, että vihreälläkin on vain yksi 0. Tässä kohtaa on siis selvää, mitkä 0 ja 2 kuuluvat toistensa kanssa samaan ryhmään. Tällä kertaa tästä ei kuitenkaan selviä vielä mitään. Jokaiseen 2-0 pariin voi valita useampia eri ykkösiä.

3-0 -jonot:

Luvuista 0 ja 3 koostuva jono voi esiintyä kahdella tavalla (sekä pelikuvat ja kierrot):

0300

03
 00

Vaikka ei voida sanoa varmaksi, mitkä nollat kuuluvat luvun 3 kanssa samaan ryhmään, 00-puolella olevista se, joka on lähempänä 3:a, kuuluu varmasti, koska nollia tarvitaan 2. Molemmissa vaihtoehdoissa kyseinen nollan on pakko olla mukana.

*Esimerkkitilanne: *

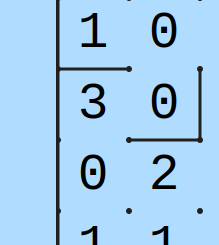
Esimerkkipeli (L18/40)

Edellä olevia sääntöjä ja muita päättelyketjuja soveltamalla voidaan asettaa (ainakin) seuraavat viivat:

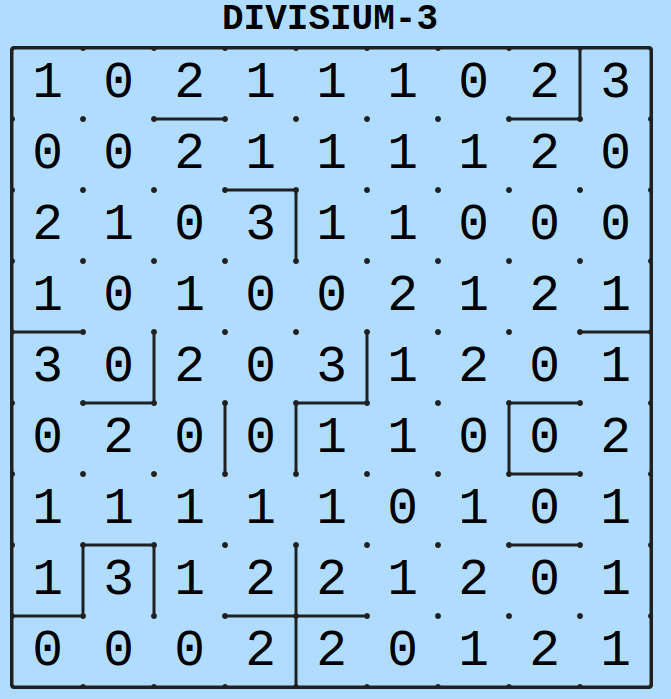
Esimerkiksi oikean yläreunan nollarykelmää voisi vielä rajata.

Tästä voi tehdä selviä päätelmiä jo melko paljon:

• Vasemman alanurkan [0,0,3] ryhmä on ilmiselvä. Alarivin kolmas 0 ei voi kuulua samaan ryhmään, koska silloin kulmaan jäisi yksinäinen 0.
• Vasemman alakulman luvun 3 vasemmalla puolella olevan luvun 1 on pakko muodostaa ryhmä [1,1,1].
• Vasemmasta alareunasta laskettuna ensimmäinen 2 on pakko muodostaa ryhmä [0,1,2]. Tästä taas seuraa, että sen yläpuolella oleva 2 on mahdollista kytkeä vain yhteen 0:aan ja näiden kahden väliin jäävään lukuun 1.
• Oikeassa yläkulmassa on selvä [3,0,0].
• Oikeassa laidassa olevan “Nollatornin” toiseksi alimmainen 0: Tämän voisi kytkeä [0,1,2]-ryhmään kahdella tavalla. Kuitenkin nähdään, että jos tämä kytketään oikean reunan kakkoseen, yksinäinen 0 jää jumiin, kun se on jo valmiiksi kolmen muun seinän sisällä. Tällöin aikaisemmin mainittu 0 onkin pakko kytkeä vasemmalla alaviistossa olevaan kakkoseen.

Jos peli kiinnostaa vielä, se löytyy osoitteesta https://vesatimonen.github.io/divisium-3/

Ratkaisija

Pelaaminen on toki hauskaa, mutta ohjelmointi voi olla vielä hauskempaa. JavaScript-versiota en tehnyt, mutta javalla ohjelmoimani versio käyttöohjeineen löytyy gitlabista: Divisium-3

Toimintaperiaate:

1. Kartoita jokaiselle ruudulle kaikki mahdolliset ryhmät, joihin kyseinen ruutu voisi kuulua.
2. Kokeile ryhmien yhdistelmiä rekursiivisesti ahneella syvyyshaulla, kunnes ruudukko on täynnä.

Vaihe 2 tarkemmin:

1. Käy pelialue läpi ruutu kerrallaan.
   1. Jos nykyinen ruutu on jo osa jotakin ryhmää, siirry seuraavaan ruutuun.
   2. Jos ei, valitse nykyiselle ruudulle ensimmäinen sopiva ryhmä, joka on vielä mahdollista listätä ilman päällekäisyyksiä.
   3. Jos ei ole mahdollista, nykyistä ruutua ei enää saada mihinkään ryhmään. Jokin edellisistä siirroista oli väärä. Peruuta edellinen siirto ja kokeile sen tilalle uutta ryhmää. Palaa tarvittaessa useampia siirtoja takaisin päin, kunnes kaikki on kokeiltu.
2. Lopeta, kun kaikki ruudut kuuluvat johonkin ryhmään, tai jos ratkaisua ei löydy.